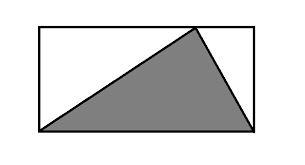
 This year, I decided to take a new course offered at my college, called Teaching Elementary Math. I expected that it would address each word in the title uniquely, but I hadn't expected to learn about teaching math in an imaginative, inspiring way. This past week, through our assigned readings and class lecture, I realized that math is much more based on unreal things than reality. For this reason, math needs to be taught in a different way that most people teach it now. When people think about math, they usually think about formulas, problems, and boring class lectures. They associate math with something tangible, objectively correct, and sterile. That is probably because the math which non-majors usually are exposed to is pointed towards two main purposes: 1. To teach children how to do basic arithmetic, and 2. To tangibly test schools and the ability of teachers through standardized tests. Although these two things are appealing, there is a beauty in math as a creative, abstract art, which often times gets forgotten. In math, we are forced to think of things differently. A large part of math deals with the imaginary world. In calculus II, students are asked to find the area of infinite curves rotated around axis. This sounds crazy! But there are actual, correct answers to this question. But even more on the basic level, we have to use our imagination to find more basic answers to elementary questions. Think about a triangle for a minute. How do we find it's area? Instead of thinking of the formula, or exiting out of this blog to google it, think about how we would get the area from areas of shapes similar to the triangle. Surround the triangle with a rectangle, so that the triangle is completely encaptured. The height of the rectangle is the same as the height of the triangle, and the widths and lengths also equate. Now, draw a line down the height of the triangle, and what do you have? Two boxes split down completely in the middle, making sense of our formula, 1/2bh. We had to think about math in a different way than normal, coming up with a more imaginative way to solve the problem than just regurgitating the formula and plugging away numbers. In the classroom, we discussed how to apply this different way of teaching math so that the students are engaged and challenged. My professor showed us that the best way to challenge the students is to teach math through the Socratic method, asking guiding questions so that the student ends up learning the desired material more organically instead of having it thrown to them. In this way, learning becomes slightly hidden, and the student will hopefully understand why specific theorems in math make sense. My professor suggested that each class begin with a question that should be challenging but doable, with its discovery as directly related with the larger topic of class. Through engaging with the students, the professor guides the students through their thoughts and helps them learn how to use their imagination to understand the class topic. Although it is important to be able to know formulas for quick arithmetic, being able to understand them and why they are important is so special, it is sad that math has been quantified and subjected to standardized testing. With so much pressure to teach students about formulas and drills, teachers may easily forget that math is beautiful too. It is like music. When we just see notes on the sheets, we can add them up to count how many beats fall in a measure. But when we play the music, the notes pluck at our heartstrings and we are forever changed.
4 Comments
Ally
6/18/2019 03:55:34 pm
I loved your post! Wow! I love this way of looking at math. I am a homeschool mom and I'm looking to lead math socratically for this coming school year. How do I learn this? What kinds of books did you use at Hillsdale? Any books specifically with regard to explaining formulas in such a way as to bring them to life? Thank you for your help!
Reply
Rossana
11/6/2022 04:15:57 am
classical has a course about teaching math using the Socratic method. I plan to take it myself this month. I teach math at a classical academy in Houston.
Reply
Rossana
11/6/2022 04:18:47 am
I meant to write classicalU.com
Heath
8/24/2022 08:41:03 pm
Ditto to first comment
Reply
Leave a Reply. |
Jessica De GreeJessica teaches 5th grade English and History as well as 11th grade Spanish III at a Great Hearts Academy in Glendale, AZ. In addition to teaching, she coaches JV girls basketball and is a writing tutor for The Classical Historian Online Academy. Jessica recently played basketball professionally in Tarragona, Spain, where she taught English ESL and tutored Classical Historian writing students. In 2018, she received her Bachelor's degree in English and Spanish from Hillsdale College, MI. Archives
April 2020
Categories
All
|
|
SUPPORT
|
RESOURCES
|
|


 RSS Feed
RSS Feed



